• ← Previous
• Next →

Counting sort is a linear time sorting algorithm. As we know, any linear time sorting algorithm has a time complexity of O(N). But to achieve linear time complexity, there are some assumptions that we make. First, the input data set is a list of non-negative numbers. Second, the range of numbers in the give data set is small and is known.

Counting sort goes through the entire array. There are no comparisons done while passing through the array. The output of counting sort is an auxiliary array of the same size. By using the original array and the auxiliary array, a new array is created with has the sorted list. This algorithm requires extra space, hence counting sort works better when the input data set is small and defined.

Let us see how the counting sort algorithm works using an example. Here is an array we would like to sort: {8, 4, 2, 2, 2, 9, 7}. The example has three phases.

In phase one, we build a count array (count_array) from the input array (input_array). The count_array is another array with size equal to the max element in the input data set. We go through input array once, and update the corresponding count in the count_array. The key thing here is that the value present in the input array corresponds to the index of the count_array. For example, we can see that there are 3 occurrences of the element with value 2 and hence the index 2 of the count_array has a value of 3.

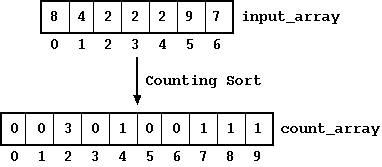
Figure: Counting Sort: Building the Count Array

In the next phase, we use the count array to create a sum array. The sum array could be another array -- we could overwrite the count_array as well. For the sake of simplicity, we keep them as two different arrays. The basic idea behind with the sum array is that at any given index, the number of elements prior to that index would be indicated by the value of the sum array at that index. Thus, in the following figure, sum_array[2] = 3 means that there are 3 elements lesser or equal 2. Similarly, sum_array[4] = 4, implies, there are 4 elements in the array that are lesser or equal to 4.

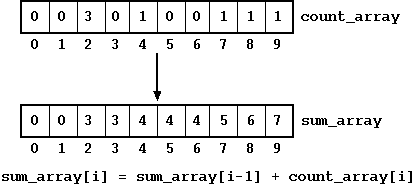
Figure: Counting Sort: Building the Sum Array

Next, we show the final step in the algorithm, where we construct another auxiliary array (result_array) that will have all the elements in sorted order. The result_array will be of the same size as the input array. The figure shows the first iteration, where we start with the last element in the input_array -- in this case that would be the element with value 7. Next, we look for the value pertaining to index 7 in the sum_array -- the value determines the index in the result_array, where we would keep 7. Once the element is placed in the result_array, we decrement the value in the sum_array. Thus, at the end of the first iteration, one element is positioned correctly. The entire result array is fully sorted at the end of the full iteration.

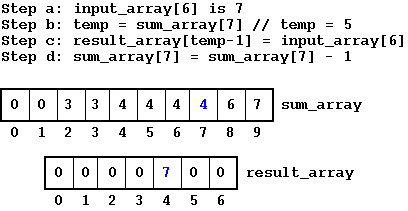
Figure: Counting Sort: Building Results Array from Sum Array -- First Iteration

Implementation

Let us now look at the implementation. As described earlier, the counting_sort() function runs three loops. The first loop builds the count_array, the second loop builds the sum_array, and the last loop builds the result_array; it is the result_array that holds the element in the sorted order.

 #include <stdio.h>

 #define MAX_ELEMENT_SIZE 9
 #define MAX_AUX_ARRAY_SIZE  (MAX_ELEMENT_SIZE + 1)

 int count_array[MAX_AUX_ARRAY_SIZE]; 
 int sum_array[MAX_AUX_ARRAY_SIZE];

 void counting_sort_init () {
     int i;

     for (i = 0; i < MAX_AUX_ARRAY_SIZE; i++) {
         count_array[i] = 0;
         sum_array[i] = 0;
     }
 }

 void counting_sort (int array[], int size) {
     int result_array[size];
     int i, j, temp;

     counting_sort_init();
     /* 
      * Step 1 : Counting the each occurrence of the element
      * in the original array 
      */
     for (i = 0; i < size; i++) {
 	count_array[array[i]] = count_array[array[i]] + 1; 
     }
     printf("\ncount_array: ");
     for (i = 0; i < size; i++) {
         printf(" %d", count_array[i]);
     }

     /* 
      * Step 2 : Populating the sum array.
      */
     for (i = 0; i < MAX_AUX_ARRAY_SIZE; i++) {
          sum_array[i] = sum_array[i - 1] + count_array[i]; 
     }
     printf("\nsum_array:   ");
     for (i = 0; i < size; i++) {
         printf(" %d", sum_array[i]);
     }

     /* 
      * Step 3 : Populating the result array.
      */
     for (i = size - 1; i >= 0; i--) {
 	temp = sum_array[array[i]];
 	result_array[temp-1] = array[i];
         sum_array[array[i]] -= 1;
     }

     printf("\nresult_array:");
     for (i = 0; i < size; i++) {
         printf(" %d", result_array[i]);
     }
     printf("\n");
 }

 int main (int argc, char *argv[]) {
     int input_array[] = { 8, 4, 2, 2, 2, 9, 7 };
     int len = sizeof(input_array)/sizeof(input_array[0]);
     int i;

     printf("input_array: ");
     for (i = 0; i < len; i++) {
         printf(" %d", input_array[i]);
     }

     /* Passing the array */
     counting_sort(input_array, len);
     return 0;
 }

Let us use the above code to analyze the time complexity for counting sort. We can see that we have three main for loops (excluding the ones that we have added for printing the arrays!). Thus, the running time is 3N and the time-complexity is O(N).

In the end, we compile the above file and get the output. The output (provided below) shows all four arrays.

 $ gcc counting_sort.c -o counting_sort
 $ ./counting_sort
 input_array:  8 4 2 2 2 9 7
 count_array:  0 0 3 0 1 0 0
 sum_array:    0 0 3 3 4 4 4
 result_array: 2 2 2 4 7 8 9
 $

• ← Previous
• Next →