Linear Sorting: Radix Sort
Radix sort is one of the linear sorting algorithms. As we know, under certain conditions/assumptions O(N) time complexity can be achieved with a linear sorting algorithm. For radix sort to work, the data should fulfill some requirements. First, one should know the max number (number of digits the max number has) in the give list. Second, the given data set does not contain very large numbers. Radix sort does not perform well when the numbers are large. Let us go through the radix sort algorithm step by step.
Let us look at an example to understand radix algorithm. For that we start with an input array. In the first step, we look at the least significant digit in every number and place (enqueue) it in the appropriate bucket (queue). We have 10 buckets, one for each digit (0 - 9). Once done, we dequeue the buckets and replace the array in the same order. This is how the array looks like at the end of step 1.
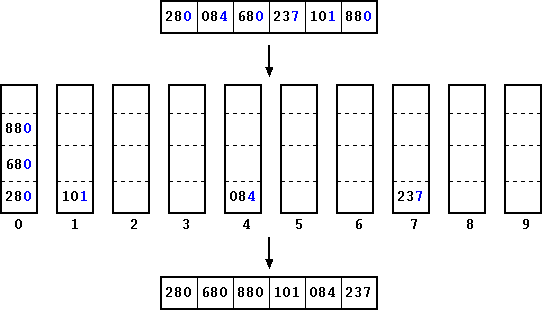
Figure: Radix Sort: Step 1
In the next step, we look at the second least significant digit in every number and place it in the appropriate bucket. Once that is done, we once again dequeue the buckets and replace the array in the same order. This is how the array looks like at the end of step 2 We reuse the set of buckets from the earlier step.
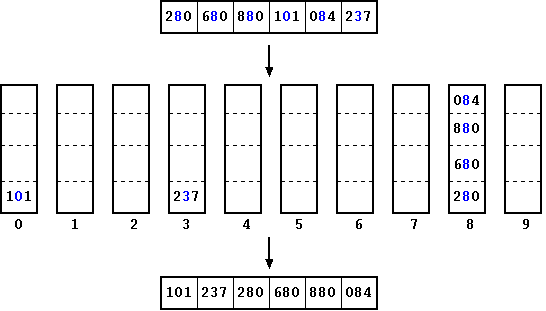
Figure: Radix Sort: Step 2
In the last step, we look at the third least significant digit (In this case Most Significant Digit (MSD)) in every number and place it in the appropriate bucket. Once that is done, we repeat the step of dequeuing buckets and replacing the array in the same order. This is how the array looks like at the end of step 3 and at the end of this step, the array would be sorted. Once again, we reuse the same set of buckets from the earlier steps.
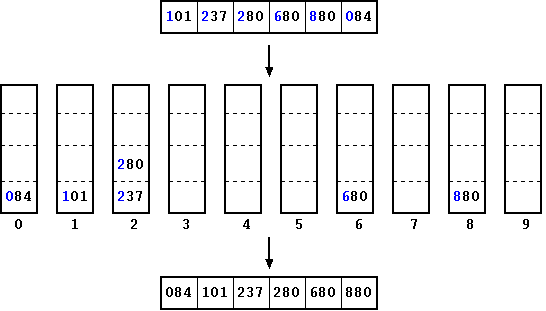
Figure: Radix Sort: Step 3
Implementation
Next, we provide an implementation of the radix sort. As described earlier, radix sort has the same number of iterations as there are the number of digits in the largest number. For each iteration, the implementation walks through all the numbers present in the input_array and puts them in each bucket. The numbers are placed in the bucket based on the digit value for that number and are placed in the bucket that has the same index as the digit value.
Our implementation uses the Queue. data structure. We use queues to mimic buckets used in radix sort. to different sets. To keep the implementation simple, we reuse the queue implementation provided in our Data-Structure module. We recommend the reader to also go through the queue data-structure. The implementation of Queue is provided in terms of both header file and an implementation file. For queue, we use the following APIs: queue_init() to initialize the radix sort queue (aka bucket), queue_enqueue() to add an element to the queue, and queue_dequeue() to pop an element from the queue.
#include <stdio.h>
#include "queue.h"
#include <math.h>
#define MAX_DIGIT_SIZE 3
#define NO_QUEUES 10
int get_the_digit (int num, int digit) {
int temp;
temp = pow(10, (digit-1));
num = num/temp;
return (num % 10);
}
void print_queue_for_me (queue *sq, int indx) {
queue_elem *elem = NULL;
printf("Printing Bucket (index: %d): ", indx);
for (elem = sq->head; elem != NULL; elem = elem->next) {
printf("%d ", *(int *)(elem->data));
}
printf("\n");
}
void radix_sort (int input_array[], int len) {
int unsorted_array[len];
int i, j, k, m, array_index = 0;
int qsize, temp, temp_val;
int error_no;
int *ret_val;
/* 10 Buckets, one for each digit 0-9 */
queue q[NO_QUEUES];
/* Init all the buckets */
for (i = 0; i < NO_QUEUES; i++) {
queue_init(&(q[i]));
}
/* Loop through the array for LSD's ( Least significant digit ) */
for (i = 1; i <= MAX_DIGIT_SIZE; i++) {
array_index = 0;
for (j = 0; j < len; j++) {
temp = get_the_digit(input_array[j], i);
queue_enqueue(&(q[temp]), (void *)&(input_array[j]));
}
for (m = 0; m < NO_QUEUES; m++) {
print_queue_for_me(&(q[m]), m);
}
/* Dequeue all the queue's and fill the array */
for (j = 0; j < NO_QUEUES; j++) {
ret_val = (int *)queue_dequeue(&(q[j]), &error_no);
while (error_no != QUEUE_ERRNO_EMPTY ) {
unsorted_array[array_index] = *ret_val;
array_index++;
ret_val = (int *)queue_dequeue(&(q[j]), &error_no);
}
}
/* Here is the reason for using an arbitrary array
* "unsorted_array instead of using same array "array".
*
* Since, the address of the original array is sent to
* the enqueue api "queue_enqueue", we might end up
* overwriting the array after dequeuing. To be on the
* safer side, an arbitrary array is used.
*/
for (k = 0; k < len; k++) {
input_array[k] = unsorted_array[k];
}
printf("After Iteration %d: ", i);
for (m = 0; m < len; m++ ) {
printf("%d ", input_array[m]);
}
printf("\n\n");
}
}
int main (int argc, char *argv[]) {
int input_array[] = {280, 84, 680, 237, 101, 880};
int len = sizeof(input_array)/sizeof(input_array[0]);
int i;
printf("Input Array:");
for( i = 0; i < len; i++ ) {
printf(" %d", input_array[i]);
}
printf("\n\n");
radix_sort(input_array, len);
printf(" \n");
return 0;
}
The time complexity of this algorithm is O(kN), where k is the number of digits in the max/highest element and N is the number of elements in the array. Number of iterations/steps before the input array is sorted is equal to k. Let us look us the implementation.
To run the above file, we use "gcc" for compiling the above file along with the "queue.c" as well. The files queue.h and queue.c files can be downloaded from our queue module. Notice the use of "-lm" at the end, -lm is used to link our program with the "math.h" library. We provide the output below. The output shows the value of the array after each iteration. It also shows the elements in each bucket at the end of each iteration.
user@codingtre $ gcc radix.c queue.c -lm -o radix.o user@codingtre $ ./radix.o Input Array: 280 84 680 237 101 880 Printing Bucket (index: 0): 280 680 880 Printing Bucket (index: 1): 101 Printing Bucket (index: 2): Printing Bucket (index: 3): Printing Bucket (index: 4): 84 Printing Bucket (index: 5): Printing Bucket (index: 6): Printing Bucket (index: 7): 237 Printing Bucket (index: 8): Printing Bucket (index: 9): After Iteration 1: 280 680 880 101 84 237 Printing Bucket (index: 0): 101 Printing Bucket (index: 1): Printing Bucket (index: 2): Printing Bucket (index: 3): 237 Printing Bucket (index: 4): Printing Bucket (index: 5): Printing Bucket (index: 6): Printing Bucket (index: 7): Printing Bucket (index: 8): 280 680 880 84 Printing Bucket (index: 9): After Iteration 2: 101 237 280 680 880 84 Printing Bucket (index: 0): 84 Printing Bucket (index: 1): 101 Printing Bucket (index: 2): 237 280 Printing Bucket (index: 3): Printing Bucket (index: 4): Printing Bucket (index: 5): Printing Bucket (index: 6): 680 Printing Bucket (index: 7): Printing Bucket (index: 8): 880 Printing Bucket (index: 9): After Iteration 3: 84 101 237 280 680 880