Minimum Spanning Tree: Prim's Algorithm
Prim's algorithm is a greedy algorithm that calculates the Minimum Spanning Tree (MST) of a connected graph. Each of the edge of the graph need to have weights. In terms of its core step, Prim's algorithm uses Breadth-First-Search (BFS) and that way it is quite similar to Dijkstra's algorithm. Both algorithms use a min-heap to extract the next edge with the minimum weight.
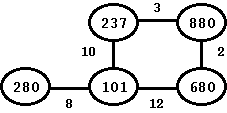
Figure: An undirected Graph with Weights
Prim's algorithm starts from an arbitrary node and then constructs a spanning tree from there. At each step, it selects a new edge and adds a new vertex from that. Thus, it grows the tree by adding a new vertex at each step. If the node is partitioned, then this algorithm would find the MST only for the partition that contains the initial arbitrary node and would ignore the other partition(s). For building MST when we have multiple partitions, we can rely on using Kruskal's algorithm for building the MST. Thus, if we were to start with above graph, the minimum spanning tree would contain the following edges: 101-280, 101-237, 237-880, and 880-680.
Prim's algorithm works by adding all the immediate edges of the current vertex into a heap. Next, it extracts the edge with the minimum weight from the heap and it finds the new vertex from this edge. This new vertex is then added to the current spanning tree and we add all of its edges to the heap. We repeat this step until all the vertices of the graph are added to the spanning tree. So, if we were to start with a source-node (let us say, 101) in the above graph, then we would start by adding this vertex to the Prim tree and adding all of its edges to the heap. Like a breadth-first search, Prim's algorithm also starts by coloring all the edges white and as it is done adding a vertex to the tree, it marks that vertex as black. Here is how the graph and the heap would look like at the first step:
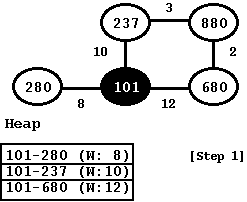
Figure: Step 1: Select source node (101) and adds its edges to Heap
Now that we have vertex 101 added to the tree, we pick the edge from the heap that has the least weight and that would be 101-280. Since 101 is already in the tree, we pick 280 and add it to the vertex. Once done we mark this vertex as black. We keep doing this till we run out of all the edges in the heap. If we find an edge in the heap such that if both of its vertices are already added, then we ignore that edge and extract the next one. We keep repeating these steps this till we have no edges left in the heap. Once done, we would see all the vertices in the graph as black. We show the remaining steps below. For clarity, we show the edges connecting the new vertex in blue.
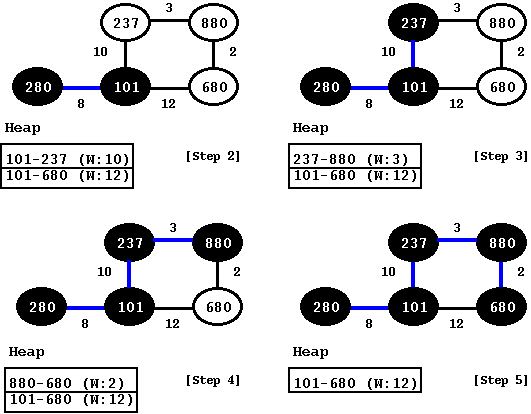
Figure: Remaining Steps: Add vertices one-by-one to the Prim tree
Implementation
Our implementation of Prim's algorithm relies on two data-structures: Adjacency List and Heap. For these structures, we reuse our implementation provided in our Data-Structure module. Reusing these structures keeps the code simple. We recommend the reader to go through these modules first.
The implementation for both adjacency list and heap are provided in terms of both header file and an implementation file. With our Prim's algorithm, we simply add the header files ("adjacency_list.h" and "heap.h") so that we can access their APIs. We use the following APIs from adjacency list: adjlist_add_vertex() to add a vertex to the adjacency list, adjlist_add_edge() to add an edge to the adjacency list, adjlist_free() to free the adjacency list, and adjlist_print() to print adjacency list. For heap, we use the following three APIs: heap_init() to initialize the heap, heap_add() to add edges to the heap, and heap_extract() to pop the edge with the smallest weight; we pass prim_heap_compare() to the heap_init() API so that we can use prim_heap_compare() to compare two of the Prim's edge nodes.
Before we go any further, let us provide the implementation. This implementation (provided below) uses a new data-structure, prim_edge_nodes that holds two vertex nodes and its weight. In addition, it also has a handful of global variables. Our implementation is structurally quite similar to our implementation of Dijkstra's Algorithm since they both use breadth-first search and have similar steps.
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include "adjacency_list.h"
#include "heap.h"
/* Represents an edge (has both sides, represented as vnode) and the edge weight. */
typedef struct prim_edge_nodes_ {
vertex_node *vnodeA;
vertex_node *vnodeB;
int weight; /* Weight of the link. */
} prim_edge_nodes;
int prim_heap_compare (const void *value1, const void *value2) {
prim_edge_nodes *node1 = (prim_edge_nodes *)value1;
prim_edge_nodes *node2 = (prim_edge_nodes *)value2;
if (node1->weight < node2->weight) {
return -1;
} else if (node1->weight > node2->weight) {
return 1;
} else {
return 0;
}
}
void prim_heap_print (heap_t *heap) {
prim_edge_nodes *node, *parent_node;
int counter = 0;
printf("Printing the Heap: \n");
if ((heap == NULL) || (heap->heap_current_size == 0)) {
printf("Heap is Empty\n\n");
return;
}
for (counter = 0; counter < heap->heap_current_size; counter++) {
node = (prim_edge_nodes *)heap->heap_array[counter];
parent_node = (prim_edge_nodes *)(heap->heap_array[(int) floor((double)(counter-1)/2)]);
if (counter == 0) {
printf("\t[i: %d] %2d-%2d (Weight: %2d Parent: NULL)\n",
counter, node->vnodeA->val, node->vnodeB->val, node->weight);
} else {
printf("\t[i: %d] %2d-%2d (Weight: %2d Parent: %d-%d)\n",
counter,
node->vnodeA->val, node->vnodeB->val, node->weight,
parent_node->vnodeA->val, parent_node->vnodeB->val);
}
}
printf("\n");
}
void prim_add_my_edges_to_heap (vertex_node *vnode, heap_t *heap) {
edge_node *enode;
prim_edge_nodes *both_enodes;
if (!vnode) {
return;
}
for (enode = vnode->list_enode; enode != NULL; enode = enode->next_enode) {
if (!(((vertex_node *)enode->parent_vnode)->color == COLOR_WHITE)) {
continue;
}
both_enodes = (prim_edge_nodes *)malloc(sizeof(prim_edge_nodes));
if (!both_enodes) {
return;
}
both_enodes->vnodeA = vnode;
both_enodes->vnodeB = enode->parent_vnode;
both_enodes->weight = enode->weight;
heap_add(heap, (void *)both_enodes);
}
}
void prim_run (vertex_node *graph_root, heap_t *heap) {
prim_edge_nodes *both_enodes, *both_enodes_prev;
vertex_node *vnode, *new_vnode, *old_vnode;
int err;
if (!graph_root || !heap) {
return;
}
/* Start by coloring all vertices as white. */
for (vnode = graph_root; vnode != NULL; vnode= vnode->next_vnode) {
vnode->color = COLOR_WHITE;
}
prim_add_my_edges_to_heap(graph_root, heap);
graph_root->color = COLOR_BLACK;
while (heap->heap_current_size) {
/* Print the Heap */
adjlist_print(graph_root);
prim_heap_print(heap);
/* Extract the Minimum */
both_enodes = (prim_edge_nodes *)heap_extract(heap, &err);
/* Find the unmarked vertex. Add its edges to Heap. */
if ((both_enodes->vnodeA) && (both_enodes->vnodeA->color == COLOR_WHITE)) {
new_vnode = both_enodes->vnodeA;
old_vnode = both_enodes->vnodeB;
}
if ((both_enodes->vnodeB) && (both_enodes->vnodeB->color == COLOR_WHITE)) {
new_vnode = both_enodes->vnodeB;
old_vnode = both_enodes->vnodeA;
}
/* This vertex would be added to MST. Mark it black. */
if (new_vnode && old_vnode) {
new_vnode->color = COLOR_BLACK;
prim_add_my_edges_to_heap(new_vnode, heap);
printf("[%s]Prim's Result: %d-%d (Weight: %d)\n",
__FUNCTION__, new_vnode->val, old_vnode->val, both_enodes->weight);
}
free(both_enodes);
new_vnode = old_vnode = NULL;
}
}
int main () {
heap_t heap;
int vertices[] = {101, 237, 680, 280, 880};
int edges[][3] = {{101, 680, 12}, {101, 237, 10}, {880, 680, 2},
{101, 280, 8}, {237, 880, 3}};
vertex_node *graph_root = NULL; /* Root of the graph */
vertex_node *vnode = NULL;
int len, i;
/* Initialize the heap. */
heap_init(&heap, prim_heap_compare);
/* Add the vertices. */
len = sizeof(vertices)/sizeof(vertices[0]);
for (i = 0; i < len; i++) {
adjlist_add_vertex(&graph_root, vertices[i], NULL);
}
/* Add the edges. */
len = sizeof(edges)/sizeof(edges[0]);
for (i = 0; i < len; i++) {
adjlist_add_edge(graph_root, edges[i][0], edges[i][1], edges[i][2]);
}
adjlist_print(graph_root);
/* Run the Prim's Algorithm. */
prim_run(graph_root, &heap);
/* Done with the Adjacency List and Heap. Free them */
adjlist_free(&graph_root);
}
The first thing the main() function does is builds an adjacency list for the graph based on the two arrays: vertices and edges. As their name suggests, these array hold the vertices and edges for the graph respectively. The edge entries also contain the weight for each edge. Once it is done, the main() function calls prim_run() to run the Prim's algorithm.
The prim_run() starts by coloring all the vertices as white. The color helps us identify if we have already added the vertex node to the tree. Next, it starts with a source vertex and marks it black. Following that, it adds all of its edges to the heap using prim_add_my_edges_to_heap(). Following that, it extracts the edge from the heap that has the minimum edge; since the heap is a min-heap, the heap extract would automatically return the minimum edge.
We repeat the steps till we no longer have any elements in the heap. As long as one of the vertex of the extract edge is white in color, we keep adding the edge. If we extract an edge and both of its vertices are black, then we ignore that edge and continue.
Now that we have put together all of the functions and the main function, let us go ahead and compile the program and run it. For that we use the gcc compiler and pass all the C files as arguments. We also add "-lm" option to tell the linker to link the maths module. The output (using the -o) option is the "prim" executable and then we run it. The output confirms the steps discussed earlier.
user@codingbison$ gcc prim.c adjacency_list.c heap.c -lm -o prim user@codingbison$ ./prim [adjlist_print] Print the Adjacency List Vertex [101][Color: 0]: -- Edge [680 (12)] -- Edge [237 (10)] -- Edge [280 (8)] Vertex [237][Color: 0]: -- Edge [101 (10)] -- Edge [880 (3)] Vertex [680][Color: 0]: -- Edge [101 (12)] -- Edge [880 (2)] Vertex [280][Color: 0]: -- Edge [101 (8)] Vertex [880][Color: 0]: -- Edge [680 (2)] -- Edge [237 (3)] [adjlist_print] Print the Adjacency List Vertex [101][Color: 3]: -- Edge [680 (12)] -- Edge [237 (10)] -- Edge [280 (8)] Vertex [237][Color: 1]: -- Edge [101 (10)] -- Edge [880 (3)] Vertex [680][Color: 1]: -- Edge [101 (12)] -- Edge [880 (2)] Vertex [280][Color: 1]: -- Edge [101 (8)] Vertex [880][Color: 1]: -- Edge [680 (2)] -- Edge [237 (3)] Printing the Heap: [i: 0] 101-280 (Weight: 8 Parent: NULL) [i: 1] 101-237 (Weight: 10 Parent: 101-280) [i: 2] 101-680 (Weight: 12 Parent: 101-280) [prim_run]Prim's Result: 280-101 (Weight: 8) [adjlist_print] Print the Adjacency List Vertex [101][Color: 3]: -- Edge [680 (12)] -- Edge [237 (10)] -- Edge [280 (8)] Vertex [237][Color: 1]: -- Edge [101 (10)] -- Edge [880 (3)] Vertex [680][Color: 1]: -- Edge [101 (12)] -- Edge [880 (2)] Vertex [280][Color: 3]: -- Edge [101 (8)] Vertex [880][Color: 1]: -- Edge [680 (2)] -- Edge [237 (3)] Printing the Heap: [i: 0] 101-237 (Weight: 10 Parent: NULL) [i: 1] 101-680 (Weight: 12 Parent: 101-237) [prim_run]Prim's Result: 237-101 (Weight: 10) [adjlist_print] Print the Adjacency List Vertex [101][Color: 3]: -- Edge [680 (12)] -- Edge [237 (10)] -- Edge [280 (8)] Vertex [237][Color: 3]: -- Edge [101 (10)] -- Edge [880 (3)] Vertex [680][Color: 1]: -- Edge [101 (12)] -- Edge [880 (2)] Vertex [280][Color: 3]: -- Edge [101 (8)] Vertex [880][Color: 1]: -- Edge [680 (2)] -- Edge [237 (3)] Printing the Heap: [i: 0] 237-880 (Weight: 3 Parent: NULL) [i: 1] 101-680 (Weight: 12 Parent: 237-880) [prim_run]Prim's Result: 880-237 (Weight: 3) [adjlist_print] Print the Adjacency List Vertex [101][Color: 3]: -- Edge [680 (12)] -- Edge [237 (10)] -- Edge [280 (8)] Vertex [237][Color: 3]: -- Edge [101 (10)] -- Edge [880 (3)] Vertex [680][Color: 1]: -- Edge [101 (12)] -- Edge [880 (2)] Vertex [280][Color: 3]: -- Edge [101 (8)] Vertex [880][Color: 3]: -- Edge [680 (2)] -- Edge [237 (3)] Printing the Heap: [i: 0] 880-680 (Weight: 2 Parent: NULL) [i: 1] 101-680 (Weight: 12 Parent: 880-680) [prim_run]Prim's Result: 680-880 (Weight: 2) [adjlist_print] Print the Adjacency List Vertex [101][Color: 3]: -- Edge [680 (12)] -- Edge [237 (10)] -- Edge [280 (8)] Vertex [237][Color: 3]: -- Edge [101 (10)] -- Edge [880 (3)] Vertex [680][Color: 3]: -- Edge [101 (12)] -- Edge [880 (2)] Vertex [280][Color: 3]: -- Edge [101 (8)] Vertex [880][Color: 3]: -- Edge [680 (2)] -- Edge [237 (3)] Printing the Heap: [i: 0] 101-680 (Weight: 12 Parent: NULL)