Adjacency Lists: Advanced Implementation
There are two common ways to represent a graph: adjacency list and adjacency matrix. This page discusses adjacency list. An adjacency list allows us to represent both vertices and edges of a graph. Adjacency list uses two types of linked lists. all the vertices are added using a linked list. Second, all of the edges that belong to a vertex are added in another linked list that is based off of that vertex. If a vertex does not have any edges, then the linked list for edges would be empty.
Before we go further, let us see how a graph looks like. Well, to put it simply, we can consider a graph to be a collection of vertices and edges. We provide a simple (undirected) graph that has 5 vertices and 4 edges; each vertex is identified by a number.
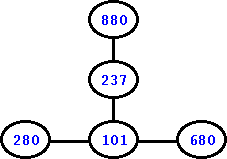
Figure: An undirected Graph
The adjacency list for the above graph starts with a linked list for vertices -- this list would have all the 5 vertices. Further, for each vertex, the representation would also have all the edges that are connected to them. As an example, the vertex 280 has one edge: 280-101. So, for the vertex 280, we would see that its linked-list for edges would have one entry: 101. Please note that for an undirected graph, every edge would show up twice in the graph, one time with each vertex. Thus, 280-101 edge would mean an edge of 101 added to the vertex 280 and an edge of 280 added to the vertex 101. This is how the adjacency list would look like for the above graph.
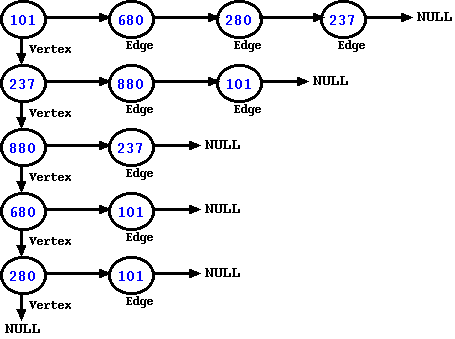
Figure: Adjacency list Representation
Besides undirected graphs, a graph can also additional behavior as well.
The graph can also have loops. In this case, we would have edges connected to each other so that it forms a loop. In the above example, if we were to add an edge between 680 and 880 vertices, then we would have a loop. An adjacency list can accommodate graphs with loops. As an extreme case, it is possible that we can have loops that start on a vertex and end at the same very vertex. For example, if we had an edge starting at vertex 101 and ending at 101, then we would have a loop starting at 101 and ending at 101.
The graph can also have directed edges. In that case, it is not a given that one can go in either direction. In the above example, if we were to make the edge 101-680 undirected such that we can go only from 101 to 680, then the picture would have an arrow going from 101 to 680. In terms of adjacency list, we would have 680 edge-node added to vertex 101, but we would not add edge-node 101 to vertex 680.
Advanced Implementation
In terms of data-structures, the adjacency list implementation should offer data structures for both edges and vertices. In terms of functionality, the implementation should offer APIs for adding vertices, adding edges, at the very least. We start by providing the implementation and go over is details after that.
Before we get into the implementation, we would like to note that the implementation on this page has various elements so that it becomes generic and dense. If you would like to see an implementation that is simpler, then you can find it here: Simple Implementation of Adjacency List.
Our implementation consists of three files: (a) a header file that publishes the data-structures and the APIs, (b) a C file that contains the implementation of the published APIs, and (c) another C file that contains the main() routine and uses the adjacency list implementation. When we use this implementation for various applications, having the implementation in three different files allows applications to reuse the header file and the implementation file.
Our implementation provides various APIs (public functions) for doing various basic operations for adjacency list. The adjlist_add_vertex() takes a value and then adds a vertex with that value to the graph. The adjlist_add_edge() takes values of the two vertices and the edge weight. The implementation also has adjlist_free() function that frees up all vertices and edges belonging to the graph. Lastly, adjlist_print() prints all the vertices and edges belonging to the graph -- we can use this to dump all edges and vertices belonging to a graph.
adjlist_add_vertex(): Add a Vertex to an Adjacency List adjlist_add_edge() : Add an Edge (with weight) to the Adjacency List adjlist_free() : Free the Adjacency List adjlist_print() : Print the Adjacency List
Let us begin with the header file. We provide the file below; we will go over its description after that.
#ifndef __ADJACENCY_LIST_H___
#define __ADJACENCY_LIST_H___
#define COLOR_WHITE 1
#define COLOR_GRAY 2
#define COLOR_BLACK 3
typedef struct vertex_node_ {
int val; /* Holds an int. Can we extended, if needed. */
void *data; /* Holds satellite data associated with this vertex */
unsigned char color; /* For visited/unvisited state. */
unsigned int set_number; /* For partitioned Graphs. See Kruskal's algorithm. */
struct edge_node_ *list_enode; /* This is a linked list for all connected edges. */
struct vertex_node_ *next_vnode; /* This is the vertical linked list for all vertices. */
} vertex_node;
typedef struct edge_node_ {
void *parent_vnode; /* Pointer to the parent vertex node. */
int weight; /* Weight of the link. */
struct edge_node_ *next_enode; /* This is a linked list. */
} edge_node;
/* Add a Vertex to an Adjacency List */
void adjlist_add_vertex(vertex_node **graph_root, int current_value, void *data);
/* Add an Edge to the Adjacency List */
void adjlist_add_edge(vertex_node *graph_root, int vertexA, int vertexB, int weight);
/* Free the Adjacency List */
void adjlist_free(vertex_node **graph_root);
/* Print the Adjacency List */
void adjlist_print(vertex_node *graph_root);
#endif /* __ADJACENCY_LIST_H___ */
The above header file starts with two data structures: vertex_node for vertices and edge_node for edges. The vertex_node data-structures supports two linked lists -- one for the vertices and one for the edges belonging to a given vertex. The next_vnode pointer enables linked list for vertices and all the vertices of a graph are added to this linked list. The list_enode pointer enables linked list for all edges that belong to a given vertex.
Besides the linked list pointer (next_enode), the edge_node contains two additional members. The "parent_vnode" pointer holds the the address of the vertex node that is added to the edge list. Thus, if an edge is formed by vertices A-B, then when we add the edge to the vertex A, the parent_vnode of the edge would point to the vertex B. Likewise, when we add the edge A-B to the vertex B, the parent_vnode of the edge would point to the vertex A. Depending upon the use-case, it is possible to simplify this where the edge node contains the value (identifier) of the vertex. However, keeping a pointer allows us to have the edge node access the entire data associated with the vertex node and for cases, where we need to store more than an integer (the "val" member), a pointer would be more efficient.
The above header uses an integer for representing the identification (let us say, key) of a vertex. If need be, one can easily extend the value of the vertex to be a non-integer. Accordingly, we would need to update both adjlist_add_vertex() and adjlist_add_edge() to accept the values as non-integer and not an integer. Lastly, the adjlist_print() also assumes that the value of each vertex is an integer -- we would need to modify that as well. Our implementation also allows application to store a satellite data for each key.
The vertex_node and edge_node data-structure contain additional members for holding miscellaneous information. The vertex node has a member "color" which is used for marking the edge. Algorithms can use this to indicate the state of the vertex. Typically, we would do initialization by marking all vertices as white. For nodes that have been selected, we mark them as black. Lastly, for nodes that are being considered, we mark them as gray. The header file contains macros for all of these three colors as well. We choose to keep the color as "unsigned char" since that would accommodate up-to 256 colors and that is more than enough! The vertex_node also contains another member "set_number" -- this is used for graphs that are partitioned and we can use this value to indicate the set number that holds a vertex. Lastly, the edge_node also contains a member "weight" to indicate the weight of the edge.
Next, we provide the implementation of the adjacency list itself. Let us see the contents of the file first and then go over its description.
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include "adjacency_list.h"
bool adjlist_print_debug = true;
/* Add a Vertex to an Adjacency List */
void adjlist_add_vertex (vertex_node **graph_root, int current_value, void *data) {
vertex_node *new_vnode, *vnode;
if (!graph_root)
return;
vnode = *graph_root;
while (vnode && vnode->next_vnode) {
if (vnode->val == current_value) {
/* If the value already exists, then return. */
printf("Vertex already exists. No need to add\n");
return;
}
vnode = vnode->next_vnode;
}
if (adjlist_print_debug)
printf("[%s] Adding Vertex Node (%d)\n", __FUNCTION__, current_value);
new_vnode = (vertex_node *)malloc(sizeof(vertex_node));
if (!new_vnode) {
fprintf(stderr, "[%s] Malloc failed \n", __FUNCTION__);
return;
}
new_vnode->val = current_value;
new_vnode->list_enode = NULL;
new_vnode->next_vnode = NULL;
new_vnode->color = 0;
new_vnode->data = data;
if (!*graph_root) {
*graph_root = new_vnode;
return;
}
vnode->next_vnode = new_vnode;
}
/* Add an Edge to a Vertex */
void adjlist_internal_add_edge_to_vertex (vertex_node *first_vnode,
vertex_node *second_vnode,
int val_second_vertex, int weight) {
edge_node *enode, *prev_enode, *new_enode;
if (!first_vnode || !second_vnode)
return;
prev_enode = enode = first_vnode->list_enode;
while (enode) {
if (((vertex_node *)enode->parent_vnode)->val == val_second_vertex) {
if (adjlist_print_debug)
printf("Edge is already added to this Vertex. No need to add\n");
return;
}
prev_enode = enode;
enode = enode->next_enode;
}
new_enode = (edge_node *)malloc(sizeof(edge_node));
if (!new_enode) {
fprintf(stderr, "[%s] Malloc failed \n", __FUNCTION__);
return;
}
new_enode->parent_vnode = second_vnode;
new_enode->next_enode = NULL;
new_enode->weight = weight;
if (prev_enode) {
prev_enode->next_enode = (void *)new_enode;
} else {
/* prev_enode is NULL means new_enode is the first enode for this vertex */
first_vnode->list_enode = (void *)new_enode;
}
}
/* Add an Edge to the Adjacency List */
void adjlist_add_edge (vertex_node *graph_root, int vertexA, int vertexB, int weight) {
vertex_node *vertex_nodeA = NULL;
vertex_node *vertex_nodeB = NULL;
vertex_node *vnode;
if (!graph_root)
return;
/*
* First, find the vnode for both vertices in the edge. We will
* add an enode to both of these vnodes.
*/
for (vnode = graph_root; vnode != NULL; vnode = vnode->next_vnode) {
if (vnode->val == vertexA) {
vertex_nodeA = vnode;
}
if (vnode->val == vertexB) {
vertex_nodeB = vnode;
}
if ((vertex_nodeA) && (vertex_nodeB)) {
break;
}
}
if (!vertex_nodeA) {
printf("[%s] vertex_nodeA [%d] not found in list of vertices\n", __FUNCTION__, vertexA);
return;
}
if (!vertex_nodeB) {
printf("[%s] vertex_nodeB [%d] not found in list of vertices\n", __FUNCTION__, vertexB);
return;
}
if (adjlist_print_debug)
printf("[%s] Adding Edge (%d-%d) to the adj list\n", __FUNCTION__, vertexA, vertexB);
/* Add Edge to VertexA. When added, this edge would point to VertexB */
if (adjlist_print_debug)
printf("\t[%s] Adding Edge (%d-%d) to Vertex Node (%d) \n",
__FUNCTION__, vertexA, vertexB, vertexA);
adjlist_internal_add_edge_to_vertex(vertex_nodeA, vertex_nodeB, vertexB, weight);
/* Add Edge to VertexB. When added, this edge would point to VertexA */
if (adjlist_print_debug)
printf("\t[%s] Adding Edge (%d-%d) to Vertex Node (%d) \n",
__FUNCTION__, vertexA, vertexB, vertexB);
adjlist_internal_add_edge_to_vertex(vertex_nodeB, vertex_nodeA, vertexA, weight);
}
/* Free the Adjacency List */
void adjlist_free (vertex_node **graph_root) {
vertex_node *vnode = NULL;
vertex_node *prev_vnode = NULL;
edge_node *enode = NULL;
edge_node *prev_enode = NULL;
if (!graph_root)
return;
vnode = *graph_root;
/* Walk the list of vertex nodes. */
while (vnode) {
/* For each vertex node, walk the list of edge nodes. */
enode = vnode->list_enode;
while (enode) {
prev_enode = enode;
enode = enode->next_enode;
free(prev_enode);
}
prev_vnode = vnode;
vnode = vnode->next_vnode;
free(prev_vnode);
}
*graph_root = NULL;
}
/* Print the Adjacency List */
void adjlist_print (vertex_node *graph_root) {
vertex_node *vnode = NULL;
edge_node *enode = NULL;
printf("[%s] Print the Adjacency List", __FUNCTION__);
if (!graph_root) {
printf("\n[%s] Nothing to print. Return\n", __FUNCTION__);
return;
}
for (vnode = graph_root; vnode != NULL; vnode = vnode->next_vnode) {
printf("\n\tVertex [%3d][Color: %d]:", vnode->val, vnode->color);
for (enode = vnode->list_enode; enode != NULL; enode = enode->next_enode) {
printf(" -- Edge [%3d (%1d)]", ((vertex_node *)enode->parent_vnode)->val, enode->weight);
}
}
printf("\n");
}
In the above code, adjlist_add_vertex() is the function that adds a vertex to the adjacency list. It starts by walking the vertices linked list. If it finds an existing vertex with the same identifier (value), then it bails out. If not, then it walks to the last node of the list. If the vertex is not found, then it mallocs a new vertex node and adds it to the last vertex node and thus, extends the linked list.
The adjlist_add_edge() is the function that adds an edge to the graph. The edge consists of two vertices and so this function essentially means adding both the vertices to each other. Thus, 280-101 edge would mean an edge of 101 added to the vertex 280 and an edge of 280 added to the vertex 101. For doing that, we walk the vertex node linked list and using the passed value of the two vertices, get hold of pointers for both vertices: vertex_nodeA and vertex_nodeB. Once that is done, we call adjlist_internal_add_edge_to_vertex() to add corresponding edges to vertex_nodeA and vertex_nodeB. The adjlist_internal_add_edge_to_vertex() function is internal since we do not add it in the header file -- as a result, users of this implementation would not be able to access that function. This is okay since there is no need to expose internal functions. The adjlist_internal_add_edge_to_vertex() function walks the edge linked list and adds this new edge, if it does not exist already.
Astute readers might also notice that for adjlist_add_vertex(), we pass the graph_root as a pointer to a pointer. However, for adjlist_add_edge(), we simply pass a pointer to the graph_root. The simple reason for that is the adjlist_add_vertex() function would end up modifying the graph_root, when adding the first vertex. But, adjlist_add_edge() does no such thing and so there is no need to pass a pointer to a pointer; a regular pointer does the job just fine!
The adjlist_print() and adjlist_free() are in some ways traversal routines. They walk over each vertex and edge of the graph. While the print routine prints each one of them, the free routine frees each one of them.
One minor detail. The implementation also comes with a global boolean, adjlist_print_debug, that controls the level of debugs. If we want to have minimal debug messages, then we should set it to false.
In the end, let us provide a simple user of the adjacency list implementation. Accordingly, we add our last C file that includes the adjacency header file (let us call it, "adjacency_list.h") and then invokes its APIs to add vertices, add edges, print the adjacency list, and then in the end, free the graph. Let us provide the file first and then we would go through the details.
#include <stdio.h>
#include "adjacency_list.h"
int main() {
int vertices[] = {101, 237, 880, 680, 280};
int edges[][3] = {{237, 880, 10}, {101, 680, 4}, {101, 280, 8}, {237, 101, 2}};
int len = sizeof(vertices)/sizeof(vertices[0]);
int i;
/* Root of the graph */
vertex_node *graph_root = NULL;
/* Add the vertices. */
printf("Adding all the Vertices\n");
for (i = 0; i < len; i++) {
adjlist_add_vertex(&graph_root, vertices[i], NULL);
}
/* Print the Adjacency List before adding all the edges */
adjlist_print(graph_root);
/* Add the edges. */
printf("\nAdding all the Edges\n");
len = sizeof(edges)/sizeof(edges[0]);
for (i = 0; i < len; i++) {
adjlist_add_edge(graph_root, edges[i][0], edges[i][1], edges[i][2]);
}
/* Print the Adjacency List after adding all the edges */
adjlist_print(graph_root);
/* Done with the Adjacency List. Free it*/
adjlist_free(&graph_root);
}
The above file has two arrays, one for the vertices and one for the edges. Each element of the edge array contains three values -- one for each of the two vertices that it connects and one for the weight of that edge. Next, it calls adjlist_add_vertex() to add all of the vertices, one by one. Following that, it calls adjlist_add_edge() to add all of the edges to the previously added vertices list. To see the adjacency list, it also calls adjlist_print() after each of the steps. And in the end, it calls adjlist_free() to free the earlier allocated memory for various vertices and edges.
The ordering of adjlist_add_vertex() and adjlist_add_edge() is important. We must call adjlist_add_vertex() first since that prepares all the vertices. If we call adjlist_add_edge() without the vertices being added to the adjacency list, then we cannot add any of the edges since the underlying vertices linked list would not be ready.
For compiling the above files, we use gcc and pass both files ("main_adjacency_list.c" and "adjacency_list.c") and name the output as "adjacency". This allows us to keep the implementation separate -- the file that uses the adjacency list ("main_adjacency_list.c", in this case) implementation is kept separate from the file that provides the implementation of the adjacency list ("adjacency_list.c"). Please note that we have kept these two files along with the header file ("adjacency_list.h") in the same folder. If that were not to be the case, then we would need to provide appropriate path for the "gcc" command and when including the header file.
Here is the compilation step and the output. The output (provided below) is similar to the earlier case, except that now we see color for each vertex and weight for each edge.
user@codingbison$ gcc main_adjacency_list.c adjacency_list.c -o adjacency
user@codingbison$ ./adjacency
Adding all the Vertices
[adjlist_add_vertex] Adding Vertex Node (101)
[adjlist_add_vertex] Adding Vertex Node (237)
[adjlist_add_vertex] Adding Vertex Node (880)
[adjlist_add_vertex] Adding Vertex Node (680)
[adjlist_add_vertex] Adding Vertex Node (280)
[adjlist_print] Print the Adjacency List
Vertex [101][Color: 0]:
Vertex [237][Color: 0]:
Vertex [880][Color: 0]:
Vertex [680][Color: 0]:
Vertex [280][Color: 0]:
Adding all the Edges
[adjlist_add_edge] Adding Edge (237-880) to the adj list
[adjlist_add_edge] Adding Edge (237-880) to Vertex Node (237)
[adjlist_add_edge] Adding Edge (237-880) to Vertex Node (880)
[adjlist_add_edge] Adding Edge (101-680) to the adj list
[adjlist_add_edge] Adding Edge (101-680) to Vertex Node (101)
[adjlist_add_edge] Adding Edge (101-680) to Vertex Node (680)
[adjlist_add_edge] Adding Edge (101-280) to the adj list
[adjlist_add_edge] Adding Edge (101-280) to Vertex Node (101)
[adjlist_add_edge] Adding Edge (101-280) to Vertex Node (280)
[adjlist_add_edge] Adding Edge (237-101) to the adj list
[adjlist_add_edge] Adding Edge (237-101) to Vertex Node (237)
[adjlist_add_edge] Adding Edge (237-101) to Vertex Node (101)
[adjlist_print] Print the Adjacency List
Vertex [101][Color: 0]: -- Edge [680 (4)] -- Edge [280 (8)] -- Edge [237 (2)]
Vertex [237][Color: 0]: -- Edge [880 (10)] -- Edge [101 (2)]
Vertex [880][Color: 0]: -- Edge [237 (10)]
Vertex [680][Color: 0]: -- Edge [101 (4)]
Vertex [280][Color: 0]: -- Edge [101 (8)]