Linked List: Introduction
Linked list allows a programmer to store and process a (dynamic) set of similar data. As the name suggests, a linked list is a list of nodes that are linked together using pointers; each node (typically) uses the same data-structure and is referred to as a link. Each link also carries a next (or/and a previous) reference pointer that links it to the next node (or/and the previous node) of the linked list.
Linked list takes the concept of arrays for storing a set of similar data and extends it in a powerful way. It allows a programmer to vary the size of the "array" as and when the need arises -- a linked list can grow or shrink as the need dictates. With arrays, one needs to either specify the array size before hand (during compile time) or periodically readjust its size by allocating more memory to it (using realloc()); the latter types of arrays are also known as dynamic arrays.
For the case of dynamic arrays, if the system memory is fragmented and if we are dealing with large number of elements, then re-sizing may not even be possible since realloc() could simply fail to find a big enough contiguous piece of memory. Furthermore, if enough elements in the array are not being used, then we need to size it down, else, it would be a wasteful use of memory. Since each individual node in a linked list can have its own memory, a linked list does not run into the issue of requiring a big contiguous piece of memory for the entire linked list.
But, then nothing is free of cost! Linked lists do require an extra storage for next (and or previous) pointers. Since we need to have these pointers per node, this is essentially an overhead. And for cases, where the data itself is small, the relative overhead of pointers can be high.
As popular as they are, linked lists may not be suitable for tasks that are lookup-intensive. This is because, the node that we are looking for might be located at the very end of the link and for that we would have to traverse the entire list -- this makes the lookup time complexity equal to O(n). It is worth mentioning that arrays also suffer from the same problem.
For such lookup-intensive tasks, we should consider alternative data-structures like balanced binary tree that usually takes O(logn) for a lookup or hash tables that usually takes O(1) average time for a lookup, but the worst-case time-complexity is same as that of arrays (O(n). If you want to know more about these algorithms, we would strongly recommend picking up a good book on data-structures and algorithms -- it would be worth it!
Types of Linked List
There are various types of linked lists. Two of the commonly used linked lists are singly linked lists and doubly linked lists. For these lists, the first node is often referred to as the "head" node and the last node is often referred to as "tail" node.
In a singly linked list, one can traverse the list in only one direction. In this type of lists, each node has a pointer that lets the current node point to the next node.
In the figure below, we show a simple singly linked list, where each node is connected to the next using a "next" pointer. Since the last node does not point to any node, the next field is set to NULL.
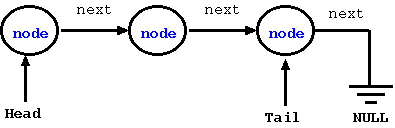
Figure: A Singly Linked List
In a doubly linked list, one can traverse the list in both directions. In this type of lists, each node has two pointers -- one pointing to the next node and an additional pointer pointing to the previous node. Needless to say, the trade-off of being able to navigate in both directions is that, now we need to keep an extra reference pointer for each node.
In the figure below, we show a simple doubly linked list, where each node is connected to its neighboring nodes using both "next" and "previous" pointers. Since the last node does not have any next node, the next field is set to NULL. Likewise, since the first node does not have any previous node, the prev field is set to NULL.
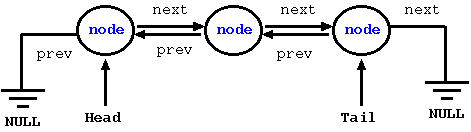
Figure: A Doubly Linked List
Another type of linked lists are circular linked lists. Such nodes are often useful for storing limited buffers such that when we are done writing all the nodes of the buffer, then the new nodes imply overwrite the existing nodes. For such cases, the head can point to the next location where we can write next buffer and the tail can point to the next location that has unread buffer. In the figure below, we present a simple circular linked list with four nodes; here, each node is connected to the next node using a "next" node.
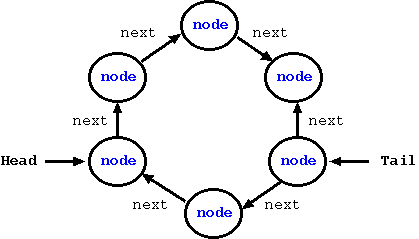
Figure: A Circular Linked List
There are other types of implementations of linked lists as well. One of them is a multiple linked list, where one node is linked to more than two other nodes in the list. In this module, we focus only on single linked list and doubly linked list.