JavaScript Functions: Memoization
Memoization technique allows us to enhance the speed of potentially slow functions by caching their arguments and results. In essence, this is a trade-off between a small amount of memory and an enhanced speed. When a memoization function is run for the first time, then it caches the results in that run. If we invoke the same function again and if the result was cached in the earlier run, then there is no need to re-run the function; instead, one can simply return the cached value.
Here is an example that shows two functions for computing factorial of a number. In the first case, there is no memoization and so if we call the factorial for 5, then the first function would be executed every time.
<!doctype html>
<html>
<div id="idDiv"></div>
<script type="text/javascript">
// Get a handle of the div element.
var elem = document.getElementById("idDiv");
var varStr = "";
// Define a recursive function to calculate factorial of a number.
function factorialSimple(num) {
varStr += "Calling factorialSimple [num: " + num + "]<br>";
if (num == 1) return 1;
return (num * factorialSimple(num-1));
}
// Invoke factorialSimple for 5.
var retVal = factorialSimple(5);
elem.innerHTML += varStr;
elem.innerHTML += "Factorial of 5 is " + retVal + "<br><br>";
// Invoke factorialSimple for 5, again!
varStr = "";
retVal = factorialSimple(5);
elem.innerHTML += varStr;
elem.innerHTML += "Factorial of 5 is " + factorialSimple(5) + "<br>";
</script>
</html>
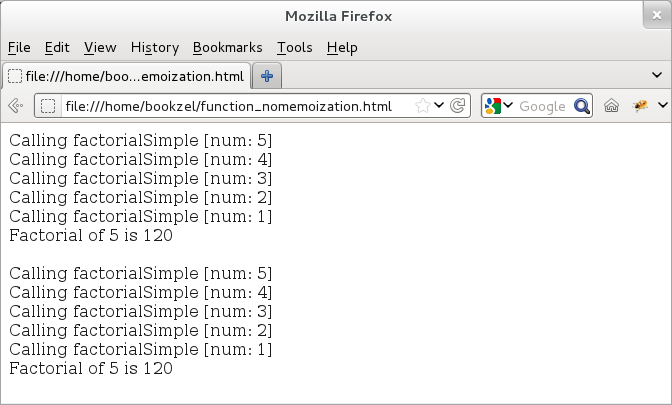
Figure: Calling a recursive function with no memoization
The second case uses memoization -- if we want to call the factorial for 5 twice, then for the second time, we can simply return the value from the cached results.
<!doctype html>
<html>
<div id="idDiv"></div>
<script type="text/javascript">
// Get a handle of the div element.
var elem = document.getElementById("idDiv");
var varStr = "";
// Create an object to cache results; initialize it with a base case of 1.
var objFactorial = {1: 1};
// Define a recursive function to calculate factorial of a number.
function factorialMemoized(num) {
varStr += "Calling factorialMemoized [num: " + num + "]<br>";
if (!(objFactorial[num-1])) {
objFactorial[num-1] = factorialMemoized(num-1);
varStr += "Storing factorial[" + (num -1)+ "] as " + objFactorial[num-1];
} else {
varStr += "Using stored factorial[" + (num -1)+ "] as " + objFactorial[num-1];
}
varStr += "<br>";
return (num * objFactorial[num-1]);
}
// Invoke factorialSimple for 5.
var retVal = factorialMemoized(5);
elem.innerHTML += varStr;
elem.innerHTML += "Factorial of 5 is " + retVal + "<br><br>";
// Invoke factorialMemoized for 5 again.
varStr = "";
retVal = factorialMemoized(5);
elem.innerHTML += varStr;
elem.innerHTML += "Factorial of 5 is " + retVal + "<br><br>";
// Print properties of factorial object.
elem.innerHTML += "Printing properties of factorial: <br>";
for (item in objFactorial) {
elem.innerHTML += "Name: " + item + ", Val: " + objFactorial[item] + "<br>";
}
</script>
</html>
And, here is the output:
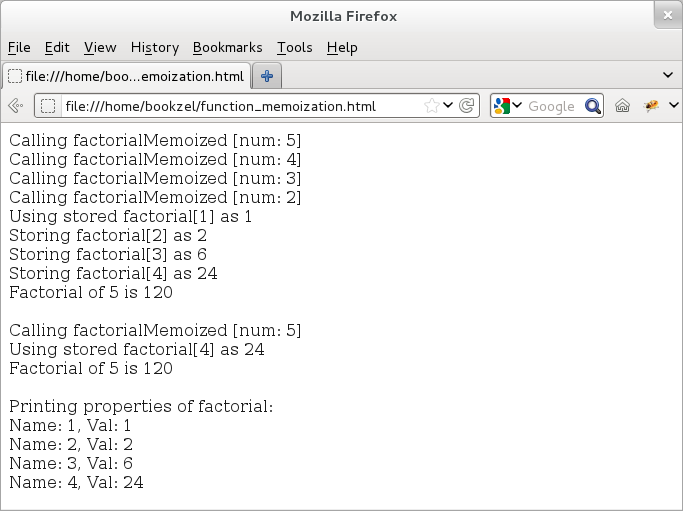
Figure: Calling a recursive function with memoization
Note that in the above example, we use "objFactorial" object to store the cached results, but since function, factorialMemoized is an object as well (recall that all functions are objects!), we can in fact use factorialMemoized to store the cached results as well!
Memoization can be applied only to those functions that exhibit same behavior when passed an identical input. This way, the memoized (stored) result would be identical to that of case when the function was run for the first time. Since recursive functions tend to re-invoke themselves by taking the next element from a series, recursive functions can usually be memoized.