Sorting: Bubble Sort
Bubble sort, like selection sort is an in place algorithm with an average time complexity of O(N^2). An, "in place" algorithm is the one where the extra space needed to the sort array is usually a small constant. Let us see how bubble sort works.
Let us say we have an array (list) of N elements to be sorted. In this technique, we will iterate through the list N times and place the largest element at the last index of an array. To achieve this, in the first iteration we compare the values at the first and the second index. If the value at the first index is greater that the value at the 2nd index, then swap them. We will keeping comparing the adjoining elements until the first iteration is completed. At the end of the first iteration ( first of the N iteration that we would do), that largest element is positioned at the end (Last index) of the array. At the second iteration ( 2nd of the n iteration) we will have the second largest element positioned at the second last position ( 2nd last index) in the array.
Let us use an example (provided below) to understand how bubble sort. For the sake of simplicity, the example shows the first iteration of bubble sort. At the end of the first iteration, we would have the largest element sitting at the last index of the array.
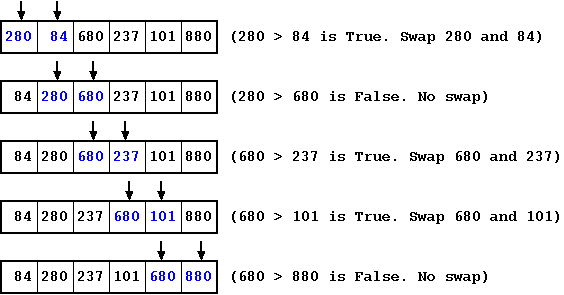
Figure: Selection Sort: First Iteration
Implementation
Let us now look at the implementation of bubble sort.
#include <stdio.h>
void print_array (int input_array[], int size) {
int i;
for (i = 0; i < size; i++) {
printf("%d ",input_array[i]);
}
}
void bubblesort (int input_array[], int size) {
int i,j,temp, swap_flag;
for (i = 0; i < size-1; i++) {
swap_flag = 0;
for (j = 0; j input_array[j+1]) {
temp = input_array[j];
input_array[j] = input_array[j+1];
input_array[j+1] = temp;
swap_flag = 1;
}
}
/* Elements in the array are in sorted order */
if (swap_flag == 0) {
break;
}
printf(" \n\tAfter Iteration %d \n\t", i+1);
print_array(input_array,size);
}
}
int main (int argc, char *argv[]) {
int i;
int input_array[] = {280,84,101,237,680,880};
int len = sizeof(input_array)/sizeof(input_array[0]);
printf("Before sorting: ");
print_array(input_array,len);
/* Call the sorting function */
bubblesort(input_array,len);
printf("\nAfter sorting: ");
print_array(input_array,len);
printf(" \n");
return 0;
}
With that, let us go ahead and run the above program. We provide the output below.
$ gcc bubblesort.c -o bubblesort $ ./bubblesort Before sorting: 280 84 680 237 101 880 After Iteration 1 84 280 237 101 680 880 After Iteration 2 84 237 101 280 680 880 After Iteration 3 84 101 237 280 680 880 After Iteration 4 84 101 237 280 680 880 After Iteration 5 84 101 237 280 680 880 After sorting: 84 101 237 280 680 880 $
In the above implementation, as you can see bubble_sort() is the function that does the sorting. This function has 2 loops, the outer loop (represented by i) shows each iteration. For each iteration we pick two consecutive elements and do the comparison. In terms of time-complexity, the bubble_sort() does N iterations and in each iteration, it compares all the N elements. Therefore, the time complexity of this algorithm is O(N^2). Bubble sort has the same complexity, whether it is worst-case or average. For a special case, where the input array is fully sorted or major part of it is sorted, the above algorithm has a complexity of O(N).
If you notice the sorting logic we compare and swap the elements only if the largest element condition is satisfied. If none of the elements are swapped in the inner loop (represented by j), then swap_flag would be 0. Thus swap_flag = 0, implies the rest of the elements in the array are already sorted. Thus we break the loop when the array is already sorted.