Sorting: Merge Sort
Sorting techniques like selection sort, bubble sort have an average time complexity is O(N^2). Let us look at a faster algorithm called Merge sort. Merge sort (like quick sort) uses divide and conquer algorithm and provides a time complexity of O(NlogN) for all three cases: average, best, and worst. Merge sort is a recursive and uses an auxiliary array to sort the elements in an array. Merge sort uses auxiliary array space that increases with the size of the input data, hence merge sort is not an in-place algorithm.
The idea behind merge sort is that at each step, we divide the array into 2 possible equal halves. Next, we recursively copy the two arrays into two other auxiliary arrays. Finally, the merge sort algorithm kicks in and sorts the 2 smaller arrays; let us call them left array and the right array. This step is a recursive call and we keep dividing the array until the base condition of the recursive function is hit, which would happen when the left array and the right array have only one element.
Once we reach the base condition, we start to merge the smaller (left and right arrays) into a bigger array. We keep merging these two arrays till we arrive back at the parent array. This would happen as unfolding of the recursion call.
We use an example to demonstrate the workings of a merge sort. The example sorts an array {84, 101, 880, 680, 237}. We show the example in two phases. In the first phase, we show how the merge_sort() recursively splits the current array into two smaller arrays. This is done till each array is of size one.
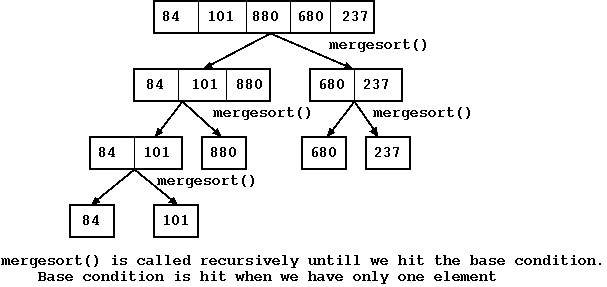
Figure: Phase 1: Merge sort()
In the second phase, we show how the merge() call allows us to take two smaller arrays and merge them into a sorted parent array. This figure essentially shows that the unfolding of the merge_sort() call since each merge_sort() call would call merge() once its child merge_sort() is complete.
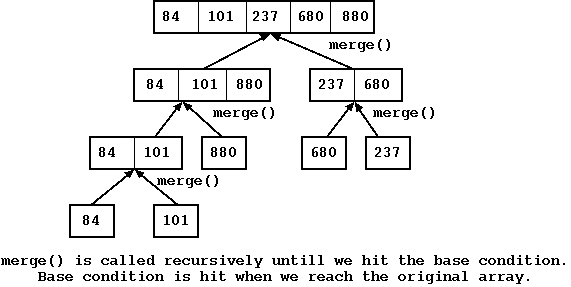
Figure: Phase 2: Merge()
Implementation
Now that we have looked at the overview of the merge sort, let us look at a simple implementation for this sorting algorithm. The implementation calls merge_sort() and passes the input array (input_array). The merge_sort function splits the array into two halves: left array and the right array. With that it calls merge_sort() again on both of the child arrays. And once the merge_sort() returns for these two child arrays, the merge_sort() calls the merge() function.
In the merge() function, we take elements from both of the child arrays and place them in a sorted order. We do this in a linear time. The while() loop continues to copy elements from one of the two arrays. To do so, it keeps separate indices for the two arrays. Let us understand this using an example. Let us say, we have left array as {84, 880} and right array as {237, 680}. The merge function will start keeping an index (in this case i for left-array and j for right-array) for two arrays; in case you are wondering, index k is for the parent array. For the left array, i would point to 84 and for the right array, j would point to 237. Since 84 is smaller than 237, we copy 84 to the parent array and increment i. Now, i points to 880. Since 880 is greater than 237, we copy 237 to the parent array and increment j. Once again, 880 is greater than the new value pointed by j (which is 680) and so we copy 680 to the parent array. Now that we are done with the right array, we would hit the second while loop -- this loop means that we are done with the right array. With that, we will continue to copy the elements (in this case only one) from the left array to the parent array. This completes the merge process.
#include <stdio.h>
void merge (int left_array[], int left_array_len,
int right_array[], int right_array_len,
int arr[], int arr_len) {
int i = 0, j = 0, k = 0, temp;
while (i < left_array_len && j < right_array_len) {
if(left_array[i] < right_array[j]){
arr[k] = left_array[i];
i++;
k++;
} else {
arr[k] = right_array[j];
j++;
k++;
}
}
/* Done with the right array. Copy elements from the left array */
while (i < left_array_len) {
arr[k] = left_array[i];
i++;
k++;
}
/* Done with the left array. Copy elements from the right array */
while (j < right_array_len) {
arr[k] = right_array[j];
j++;
k++;
}
}
void merge_sort (int input_array[], int size) {
int total_len = size;
int left_array_len = total_len/2;
int right_array_len = (total_len - left_array_len);
int left_array[left_array_len];
int right_array[right_array_len];
int i, k = 0;
if (total_len < 2) {
return;
}
for (i = 0; i < left_array_len; i++){
left_array[i] = input_array[i];
}
for (i = left_array_len; i < total_len; i++) {
right_array[k] = input_array[i];
k++;
}
merge_sort(left_array, left_array_len);
merge_sort(right_array, right_array_len);
merge(left_array, left_array_len, right_array, right_array_len, input_array, total_len);
}
int main (int argc, char *argv[]) {
int input_array[] = {84, 101, 880, 680, 237};
int len = sizeof(input_array)/sizeof(input_array[0]);
int i;
printf("Before sorting: ");
for(i = 0; i < len; i++){
printf(" %d", input_array[i]);
}
/* Passing the array */
merge_sort(input_array, len);
printf("\nAfter sorting: ");
for(i = 0; i < len; i++){
printf(" %d", input_array[i]);
}
printf("\n");
return 0;
}
From the above code, we can see that the merge_sort() splits the array into approximately two equal arrays. Thus, if the input_array has N elements, then we would do a total of logN such splits. Since at each split, we are going to process elements, the upper bound would NlogN since at each step, the maximum number of elements that we would process would be N. For merge sort, the time complexity O(NlogN) for all cases: worst case, best case, and average case. The key disadvantage with merge sort is that, it is not an in-place algorithm.
With that, let us go ahead and run the above program. We provide the output below.
$ gcc merge_sort.c -o merge_sort $ ./merge_sort Before sorting: 84 101 880 680 237 After sorting: 84 101 237 680 880