Sorting: Quicksort
Quick sort is one of the most widely used sorting algorithm. In fact sorting libraries provided by most of the programming languages are implemented as quick sort. We have seen sorting techniques like selection sort, bubble sort whose average time complexity is O(N^2). Quick sort is a faster algorithm, it has an average and best case complexity of O(NlogN) and the worst case complexity of O(N^2). With a little tweak to the basic quick sort algorithm we can almost achieve the worst case complexity as O(NlogN). Like merge sort, quick sort is also a divide and conquer algorithm. At each step it selects an element (called pivot) and then rearranges the array such that all the elements to the left of the pivot are smaller than pivot and all the elements on the right of the pivot are greater than pivot. With pivot in place, we partition the array into two arrays. The first array consists of elements that are smaller than the pivot and the second array consists of the elements that are larger than the pivot.
Quick sort is an in place algorithm and we don't use an auxiliary array like the way we use in merge sort. The extra space required by quick sort does not increase with the size of the input data set. Quick sort logic rearranges the elements with in the same array, hence quick sort is efficient in terms of memory.
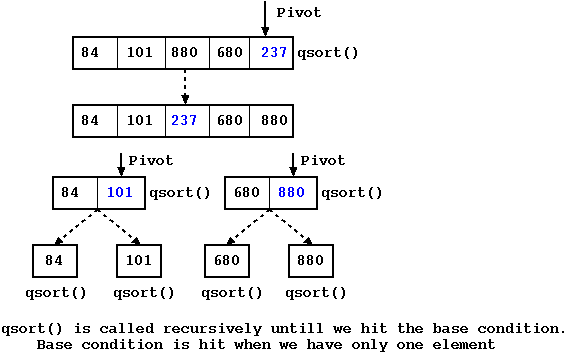
Figure: Quicksort
Implementation
In the above example, partition() function inside the quick_sort() function, selects element (237) as the pivot element and positions it, such that all the elements to the left of 237 are smaller than 237 and to the right are greater than 237. This will create 2 partitions in the array. The first partition would have index going from beginning of the current partitions till the index of 237 but not including 237. The second partition would start at the index immediately after that of 237 and would end with last index of the current partition. quick_sort() function is called recursively with these 2 partitions. For step by step procedure on how recursion works, please take a look at the recursion section in our C module.
#include <stdio.h>
void print_array (int input_array[], int size) {
int i;
for (i = 0; i < size; i++) {
printf("%d ",input_array[i]);
}
}
int partition (int input_array[], int start, int end) {
int pivot_index = start,i,temp;
/*
* Identify the correct position (pivot_index) for the pivot element.
*/
for (i = start; i < end; i++) {
/*
* Element at the last index of an array is the pivot element.
* pivot_element = input_array[end]
*/
if (input_array[i] <= input_array[end]) {
temp = input_array[i];
input_array[i] = input_array[pivot_index];
input_array[pivot_index] = temp;
pivot_index++;
}
}
/*
* Once the correct position is identified, swap the pivot element
* ( last element in the array ) with the pivot_index .
*/
temp = input_array[pivot_index];
input_array[pivot_index] = input_array[end];
input_array[end] = temp;
return pivot_index;
}
void quick_sort (int input_array[], int start, int end) {
int pivot_index;
if (start < end) {
/* Get the pivot_index */
pivot_index = partition(input_array,start,end);
quick_sort(input_array, start, pivot_index-1);
quick_sort(input_array,pivot_index+1,end);
}
}
int main (int argc, char *argv[]) {
int input_array[] = {280,84,101,237,680,880};
int len = sizeof(input_array)/sizeof(input_array[0]);
int i;
printf("Before sorting :");
print_array(input_array,len);
/* Passing the start and the end index of an array */
quick_sort(input_array,0,len-1);
printf("\nAfter sorting :");
print_array(input_array,len);
printf(" \n");
return 0;
}
Typically, in each iteration, we would split the current partition into approximately two equal partitions -- this would hold true for the average case. Thus, if the input_array has N elements, then we would do a total of logN such splits. Since at each split, we are going to process elements present in that partition, the upper bound would NlogN since at each step, the maximum number of elements that we would process would be N. Thus, for quick sort, the time complexity O(NlogN) is applicable for both best and average case. The worst case, however, is O(N^2) and we would hit this when the list is already sorted.
Let us compile the above code and get the output:
$ gcc quick_sort.c -o quick_sort $ ./quick_sort Before sorting : 84 101 880 680 237 After sorting : 84 101 237 680 880
With a little tweak to quick sort algorithm called "Randomized quick sort" the worst case complexity of O(NlogN) can be achieved almost every time. Here is the implementation of the randomized quick sort. The key to randomized quick sort is "selecting the pivot element." We do not always select the element at the last index as pivot element, instead selection of pivot index would be random.
#include <stdio.h>
void print_array (int input_array[], int size) {
int i;
for (i = 0; i < size; i++) {
printf("%d ",input_array[i]);
}
}
int partition (int input_array[], int start, int end) {
int pivot_index = start,i,temp;
/*
* Identify the correct position (pivot_index) for the pivot element.
*/
for (i = start; i < end; i++) {
/*
* Element at the last index of an array is the pivot element.
* pivot_element = input_array[end]
*/
if (input_array[i] <= input_array[end]) {
temp = input_array[i];
input_array[i] = input_array[pivot_index];
input_array[pivot_index] = temp;
pivot_index++;
}
}
/*
* Once the correct position is identified, swap the pivot element
* ( last element in the array ) with the pivot_index .
*/
temp = input_array[pivot_index];
input_array[pivot_index] = input_array[end];
input_array[end] = temp;
return pivot_index;
}
int random_partition (int input_array[], int start, int end) {
int pivot_index;
int temp;
/*
* The key difference between quick sort vs Randomized quick sort is that,
* pivot element is chosen randomly vs Last element to be the pivot element.
*/
pivot_index = (rand() % (end-start)) + start;
/* Swap the random pivot element with the last element of the array */
temp = input_array[pivot_index];
input_array[pivot_index] = input_array[end];
input_array[end] = temp;
/*
* Partition logic will remain the same, since the pivot element in the
* array is already updated.
*/
return partition(input_array,start,end);
}
void quick_sort (int input_array[], int start, int end) {
int pivot_index;
if (start < end) {
/* Get the pivot_index */
pivot_index = partition(input_array,start,end);
quick_sort(input_array, start, pivot_index-1);
quick_sort(input_array,pivot_index+1,end);
}
}
int main (int argc, char *argv[]) {
int input_array[] = {280,84,101,237,680,880};
int len = sizeof(input_array)/sizeof(input_array[0]);
int i;
printf("Before sorting :");
print_array(input_array,len);
/* Passing the start and the end index of an array */
quick_sort(input_array,0,len-1);
printf("\nAfter sorting :");
print_array(input_array,len);
printf(" \n");
return 0;
}
In the above code, function random_partition() selects the pivot element randomly and swaps it with the last element of the input array. The logic in the partition() function remains identical for both the versions of the quick sort.
With that, let us compile and run the above code. Here is the output:
$ gcc quick_sort_random.c -o quick_sort_random $ ./quick_sort_random Before sorting : 84 101 880 680 237 After sorting : 84 101 237 680 880 $